80 pie patterns

weber1929

Pie patterns are three-dimensional analogues of the much more familiar border patterns, having wallpaper patterns as their cross sections. The term is mine but the concept (‘two-sided plane’) goes back to the late 1920’s, and so does the result that there exist precisely 17+46+17=80 pie patterns: the goal of this post is to revisit this result and concept.

The standard approach to and classification of pie patterns — see section 8.8 (Notes and References to Chapter 8) of Grunbaum & Shephard’s TILINGS AND PATTERNS for details — is a combination of group-theoretic methods and concepts (that I totally avoid, even though one might for example protest that my “cross pattern” is a geometrical disguise of Coxeter’s color-preserving normal subgroup) and simple geometric facts and ideas (that I also use, for example my “level-swapping isometries” are Shubnikov’s antisymmetries). I believe that employing Geometry rather than Group Theory makes this material more accessible and revealing, and so does my notation for pie patterns, directly inspired by that for border patterns and stressing their three-dimensional nature over their two-dimensional ‘representation’. Still, it is a two-dimensional result — the existence of precisely 46 two-colored wallpaper patterns (provable by both Geometry and Group Theory) — that plays the decisive role in my current approach (and in the standard approach as well).

Every cross (‘horizontal’) section of a pie pattern is a wallpaper pattern, inheriting the restriction of the pie pattern’s ‘vertical’ isometries; at each level of the pie pattern the corresponding wallpaper patterns may be distinct, but they have to be of the same type, sharing in fact the same isometries: this type of wallpaper pattern I call “cross pattern” of the pie pattern. Further, and following the basic idea of the preceeding post, I observe that it suffices to consider pie patterns consisting of only two levels; the pie pattern’s ‘full identity’ is now determined by the cross pattern’s isometries and the isometries that swap lower level and upper level.

It is important to point out — remembering that it is isometries rather than motifs that do matter — that a cross pattern is considered as such only in case all its isometries are ‘vertically extended’ across the entire pattern; differently said, the cross pattern is a ‘valid representation’ of the pie pattern’s vertical isometries (that work, at each cross section, as isometries for a horizontal wallpaper pattern).

For example, the two $p112$ border patterns in the right column of the preceeding post do not have $m$ as their cross pattern: indeed the ‘point reflection’ of the one-dimensional pattern $m$ at the top/bottom is not extended to the entire border pattern as a vertical reflection, due to top and bottom being ‘asymetrically placed’ with respect to each other. For a pie pattern analogous situation, consider the pie pattern (right below) having copies of the same $pmm$ wallpaper pattern at both its upper level (blue rectangles) and lower level (black rectangles); the asymetrical placement of the two patterns with respect to each other has killed all the reflections and twofold rotations (‘inherited’ from the $pmm$ and the rectangles), so the resulting pie pattern has nothing but twofold rotoreflection (of axes passing through centers of ‘intersection rectangles’) — an outcome (later to be named $111\bar{2}/p1$ ) also achievable through some ‘ghost’ cross pattern of $p1$ type like the one consisting of the shown black (or blue) right triangles:
pmm-p1 [A slightly more symmetrical placement of rectangles left to the reader … would allow for vertical reflections and vertical twofold rotations, fully exploiting the $pmm$ ‘s rich structure and creating a pie pattern with horizontal glide reflection (later to be named $mab2/pmm$ and roughly corresponding to the border pattern $pma2$ ); this is not to be confused with the pie pattern — later to be named $mmr2/pmm$ and corresponding to the border pattern $pmm2$ — where the upper $pmm$ is directly above the lower $pmm$ .]

The basic symmetry possibilities for border patterns (‘horizontal’ reflection or glide reflection about the pattern’s middle line, ‘vertical’ reflection, and half turn) are now extended to ‘horizontal’ reflection ( $m$ ) or ‘horizontal’ glide reflection ( $a$ ) about the pattern’s middle plane, ‘vertical’ reflection ( $m$ ) or ‘vertical’ glide reflection of vector parallel to the middle plane ( $g$ ), twofold ( $2$ ) or threefold ( $3$ ) or fourfold ( $4$ ) or sixfold ( $6$ ) rotation about an axis perpendicular to the middle plane, AND ‘horizontal’ twofold rotation ( $r$ ) or ‘horizontal’ twofold glide rotation ( $b$ ) about an axis lying on the middle plane. Note that a twofold or a threefold vertical rotation may have a ‘square root’, that is a fourfold ( $\bar{4}$ ) or sixfold ( $\bar{6}$ ) vertical rotoreflection (the square of which yields the respective rotation), and there may also exist twofold rotoreflection ( $\bar{2}$ ), also known as inversion. (Observe that a fourfold or sixfold rotation cannot have such a ‘square root’, as the composition of two nearest parallel eightfold or twelvefold rotoreflections would yield a fourfold or sixfold rotation that would rotate the respective rotoreflection to a nearer one.)

[For background information on three-dimensional isometries I refer the reader to George Martin’s TRANSFORMATION GEOMETRY or to my own ISOMETRIES COME IN CIRCLES. (Note here that I use the term “glide rotation” instead of the better known term “screw rotation”.)]

Focusing for now on the first three possibilities for a pie pattern, that is ‘vertical’ (glide) reflection ( $m/g$ ), ‘horizontal’ (glide) reflection ( $m/a$ ), and ‘horizontal’ (glide) twofold rotation ( $r/b$ ), and denoting their absence by $1$ , we see that there exist 27 possible combinations, of which 10 are ruled out by simple geometrical arguments, yielding thus 17 ‘roots’: mmr, mar, mab, gmb, gar, gab, m1r, m1b, m11, g1r, g1b, g11, 1m1, 1a1, 11r, 11b, 111. (In the cases m1r/g1r and m1b/g1b the vertical (glide) reflection and the horizontal (glide) twofold rotation cannot be parallel to each other as the composition of a vertical (glide) reflection and a parallel to it twofold (glide) rotation yields a horizontal (glide) reflection, the ‘root’ gmr is ruled out by the fact that the composition of a horizontal reflection and a twofold rotation lying on it yields a vertical reflection, etc) Note that a g in the first position (vertical glide reflection) implies the absence of vertical reflection (m), but not vice versa: there could exist some ‘free’ glide reflection, of axis different from that of the reflection, parallel to it or not. Further, an a in the second position (horizontal glide reflection) implies the absence of horizontal reflection. (By rough analogy, the possible ‘roots’ for border patterns are mm, ma, m1, 1m, 1a, 11, allowing the well known $7$ types $pmm2$ , $pma2$ , $pm11$ , $p1m1$ , $p1a1$ , $p112$ , $p111$ .)

[Compositions of isometries can be studied in the traditional manner, that is by expressing them as compositions of reflections. Here are some useful rules (with $m/g$ , $m/a$ , $r/b$ as above and $x$ , $\bar{x}$ denoting vertical rotation and vertical rotoreflection, respectively): $m/g*m/a = r/b$ , $m/g*r/b = \bar{x}$ (when $r/b$ is not parallel to $m/g$ ), $m/g*r/b = m/a$ (when $r/b$ is parallel to $m/g$ ), $r/b*m/a = m/g$ , $m/g*x = m/g$ , $m/a*x = \bar{x}$ , $x*\bar{x} = m/a$ , $r/b*x = r/b$ , $r/b*\bar{x} = m/g$ , $m/g*\bar{x} = r/b$ .]

Note here the kinship between the horizontal (glide) reflection ( $m/a$ ) & half turn ( $2$ ) of border patterns and the horizontal (glide) reflection ( $m/a$ ) & horizontal twofold (glide) rotation ( $r/b$ ) of pie patterns: these are the isometries that swap upper level and low level! Of course in the case of pie patterns vertical rotoreflections are also ‘level-swapping’ isometries; on the contrary, the pie pattern’s vertical rotations are ‘global’ isometries, working across the entire pie patern, yielding two-dimensional rotations at each level.

In the case of two-level pie patterns, do upper level and lower level need to be congruent? In the presence of level-swapping isometries such as horizontal (glide) reflection, horizontal twofold (glide) rotation and rotoreflection, the answer is certainly “yes”; in all other cases the answer is “no”, and the lower level could be just another wallpaper pattern of same type as the upper level or simply empty! (This last observation allows us to understand the absence of a $pm11$ two-level example in the preceeding post … as well as to trivially construct one-level examples simply by deleting the lower level in the $pmm2$ and $pma2$ examples OR by slightly increasing or decreasing the length of bars at the lower level.)

In the following double example, where grey represents upper level and black represents lower level, the pie pattern on the left is of type II (later to be named $mar4/p4m$ ), with vertical reflection planes in four directions, vertical glide reflection planes containing horizontal twofold rotation axes in two (‘vertical’ – ‘horizontal’) directions, horizontal twofold glide rotation axes in two (‘diagonal’) directions, vertical fourfold rotation, vertical fourfold rotoreflection, and vertical twofold rotoreflection, whereas the pattern on the right is of type III (later to be named $m114/p4m$ ), with vertical reflection planes in four directions, vertical glide reflection planes in two (‘vertical’ – ‘horizontal’) directions, vertical fourfold rotation, and ‘free’ vertical twofold rotation. In both patterns the cross pattern is $p4m$ . In the pattern on the left, upper and lower level are congruent to each other; in the pattern on the right, upper and lower level merely share the same isometries.

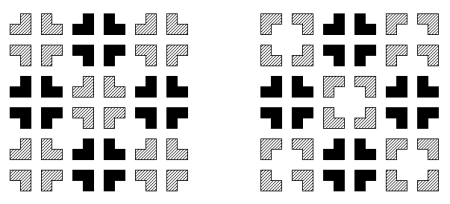
mar4-114

Our discussion so far suggests that we need three separate investigations: (I) roots mmr, gmb, 1m1 (lower level and upper level mirror images of each other) (II) roots mar, mab, gar, gab, m1r, m1b, g1r, g1b, 1a1, 11r, 11b, 111 (lower level and upper level congruent to each other) (III) roots m11, g11, 111 (lower level and upper level merely sharing the same isometries).

[Perplexed over 111‘s inclusion in (II), too? Just think of rotoreflection!]

(I) The wallpaper patterns allowed as cross patterns for the pie patterns corresponding to the roots mmr, gmb, 1m1 are — the ‘judges’ here being the first letter (vertical (glide) reflection restricted at each level to two-dimensional (glide) reflection) and the missing fourth letter (vertical rotation restricted at each level to two-dimensional rotation) — { $pm$ , $cm$ , $pmm$ , $cmm$ , $pmg$ , $p4m$ , $p4g$ , $p31m$ , $p3m1$ , $p6m$ }, { $pg$ , $pgg$ }, { $p1$ , $p2$ , $p4$ , $p3$ , $p6$ }, respectively. Note that, in the presence of horizontal reflection, every vertical rotation axis is also a vertical rotoreflection axis (and vice versa), so rotoreflection will never be mentioned in the present case. The resulting $17$ pie patterns are ‘level-by-level’ copies of the $17$ wallpaper patterns and may be listed by root as follows:

mmr (vertical reflection, horizontal reflection, horizontal twofold rotation):

$mmr1/pm$

$mmr1/cm$

$mmr2/pmm$

$mmr2/cmm$

$mmr2/pmg$

$mmr4/p4g$

$mmr4/p4m$

$mmr3/p31m$

$mmr3/p3m1$

$mmr6/p6m$

gmb (vertical glide reflection, horizontal reflection, horizontal twofold glide rotation):

$gmb1/pg$

$gmb2/pgg$

1m1 (horizontal reflection):

$1m11/p1$

$1m12/p2$

$1m14/p4$

$1m13/p3$

$1m16/p6$

(II) The wallpaper patterns possibly allowed as cross patterns for the pie patterns corresponding to the roots mar, mab, gar, gab, m1r, m1b, g1r, g1b, 1a1, 11r, 11b, 111 are, again, { $pm$ , $cm$ , $pmm$ , $cmm$ , $pmg$ , $p4m$ , $p4g$ , $p31m$ , $p3m1$ , $p6m$ } (for the roots mar, mab, m1r, m1b), { $pg$ , $pgg$ } (for the roots gar, gab, g1r, g1b), and { $p1$ , $p2$ , $p4$ , $p3$ , $p6$ } (for the roots 1a1, 11r, 11b, 111). Unlike in case (I), however, where it is obvious that all allowed types do indeed exist (by mere mirroring), here we seem destined to investigate the actual existence of $4\cdot 10 + 4\cdot 2 + 4\cdot 5 = 68$ types. Further, we would need to be careful with rotoreflection: the composition of vertical rotation and horizontal glide reflection yields a vertical rotoreflection of same order about a different axis (roots mar, mab, gar, gab, 1a1), whereas rotoreflection may also be there ‘on its own’ (roots m1r, m1b, g1r, g1b, 111 … but not 11r or 11b, as the composition of vertical rotoreflection with horizontal twofold (glide) rotation would yield vertical (glide) reflection perpendicular to the latter); in the first case only rotation is going to be indicated, with rotoreflection simply ‘implied’.

(III) The wallpaper patterns allowed as cross patterns for the pie patterns corresponding to the roots m11, g11, 111 are, exactly as in (I), { $pm$ , $cm$ , $pmm$ , $cmm$ , $pmg$ , $p4m$ , $p4g$ , $p31m$ , $p3m1$ , $p6m$ }, { $pg$ , $pgg$ }, { $p1$ , $p2$ , $p4$ , $p3$ , $p6$ }, respectively. As in (I), all $17$ predicted types are obviously possible, by placing a wallpaper pattern at the upper level and leaving the lower level empty, for example; and we can do better than that, as our $m114/p4m$ example above shows!

[By comparison, the border patterns corresponding to pie patterns of type I, II, III are { $pmm2$ , $p1m1$ }, { $p1a1$ , $p112$ , $pma2$ }, { $pm11$ , $p111$ }, respectively; again, it is type II border patterns that are the least predictable.]

In view of (II), the classification of pie patterns would promise to be quite complicated. Our two-level representation of pie patterns, however, together with an one-to-one correspondence between two-level pie patterns and two-colored wallpaper patterns established below (implicitly known since 1929), will simplify the situation significantly.

To wit, let us first recall that the 46 two-colored wallpaper patterns, first described as such in 1936 by H. J. Woods, are discussed in detail in Chapter 5 of Dorothy Washburn’s & Donald Crowe’s SYMMETRIES OF CULTURE, as well as in Chapter 6 of my own ISOMETRICA (available both in book form and online); the second source contains a detailed geometrical discussion and classification of two-colored patterns, whereas the first source is more oriented toward examples from anthropology and artwork. (I believe that my classification of the 46 two-colored wallpaper patterns in ISOMETRICA, together with those of H. J. Woods and Arthur Loeb (COLOR AND SYMMETRY), are the only geometrical ones, the others being group-theoretic.)

The promised correspondence between two-level pie patterns and two-colored wallpaper patterns is now established by coloring grey the upper level and black the lower level of a pie pattern. Unless the lower level is ‘straight below’ the upper level (as in (I) and some slightly more complicated cases discussed later), the pie pattern looks, ‘viewed from above’, like a two-colored wallpaper pattern, with the following matching betwen three-dimensional pie pattern isometries and two-dimensional wallpaper pattern isometries:

horizontal glide reflection ( $a$ ) <——> color-reversing translation ( $p'$ )

vertical reflection ( $m$ ) <——> color-preserving reflection ( $m$ )

vertical glide reflection ( $g$ ) <——> color-preserving glide reflection ( $g$ )

horizontal twofold rotation ( $r$ ) <——> color-reversing reflection ( $m'$ )

horizontal twofold glide rotation ( $b$ ) <——> color-reversing glide reflection ( $g'$ )

vertical twofold rotation ( $2$ ) <——> color-preserving twofold rotation ( $2$ )

vertical threefold rotation ( $3$ ) <——> color-preserving threefold rotation ( $3$ )

vertical fourfold rotation ( $4$ ) <——> color-preserving fourfold rotation ( $4$ )

vertical sixfold rotation ( $6$ ) <——> color-preserving sixfold rotation ( $6$ )

vertical twofold rotoreflection ( $\bar{2}$ ) <——> color-reversing twofold rotation ( $2'$ )

vertical fourfold rotoreflection ( $\bar{4}$ ) <——> color-reversing fourfold rotation ( $4'$ )

vertical sixfold rotoreflection ( $\bar{6}$ ) <——> color-reversing sixfold rotation ( $6'$ )

In other words, level-swapping pie pattern isometries are, in effect, color-reversing wallpaper pattern isometries (and vice versa)! An obvious ‘exception’ is made for the ‘invisible’ horizontal reflection, the presence of which simplifies matters greatly anyway (as already noted in (I)).

Are there other ‘exceptions’? It seems at first that we might run into problems when a vertical glide reflection plane ( $g$ ) contains a horizontal twofold rotation axis ( $r$ ), or, ‘conversely’, a vertical reflection plane ( $m$ ) contains a horizontal twofold glide rotation axis ( $b$ ): in these two cases the corresponding lines in the planar ‘symmetry plan’ would coincide, seemingly requiring a separate investigation! (Note here that the other two cases are impossible: a horizontal twofold rotation axis ( $r$ ) contained in a vertical reflection plane ( $m$ ) creates horizontal reflection ( $m*r$ ); and a horizontal twofold glide rotation axis ( $b$ ) contained in a vertical glide reflection plane ( $g$ ) is also impossible … as an equality of minimal gliding vectors would again imply horizontal reflection ( $g*b^{-1}$ ), whereas unequal minimal gliding vectors would violate the minimality of either $b$ ‘s gliding vector (via $g*b^{-1}*g$ and $|2x-y|<y$ for $x<y$ ) or $g$ ‘s gliding vector (via $b*g^{-1}*b$ and $|2y-x|<x$ for $y<x$ ).)

The ‘exceptions’ discussed above pose no problems for our perspective (pun intended), as the following example illustrates:
bem-reg
Indeed, in this example — involving separate views of the upper level (grey triangles) and of the lower level (black triangles) — the lines passing through columns of triangles represent both vertical glide reflection planes and horizontal twofold rotation axes lying on them ( $r\in g$ ), whereas the lines passing between columns of triangles represent both vertical reflection planes and horizontal twofold glide rotation axes lying on them ( $b\in m$ ). It seems at first that this example may not correspond to any two-colored types, being impossible to represent through a single planar two-colored pattern; but the following ‘unified’ pattern (later to be known as a $mar1/cm$ ) does just that, sharing the same isometries with the initial example:

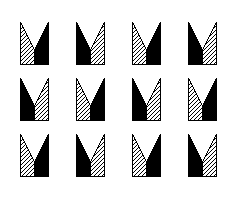
In other words, the ‘exceptional’ cases $r\in g$ and $b\in m$ simply correspond, in the context of two-colored wallpaper patterns, to the cases of a color-reversing reflection axis also being a color-preserving glide reflection axis and of a color-preserving reflection axis also being a color-reversing glide reflection axis, respectively; in both cases, color-reversing translation in the direction of (glide) reflection plays the decisive role … and implies, in the context of pie patterns, that the cases $r\in g$ and/or $b\in m$ may only occur in the presence of horizontal glide reflection ( $a$ ) and only with the roots mar, mab, gar, gab.

Below I provide examples of the $10$ two-colored wallpapern patterns that have (glide) reflection but no rotation, corresponding to the $10$ type II pie-patterns that have no vertical rotation or rotoreflection but do have vertical (glide) reflection or horizontal twofold (glide) rotation (or both); we use the pie pattern name (to be provided further below) rather than the two-colored wallpaper pattern name. The pie pattern is ‘viewed from above’, so both (glide) reflection planes and twofold (glide) rotation axes are shown in blue and red lines, respectively, whereas the cases $b\in m$ and $r\in g$ are represented by purple lines:

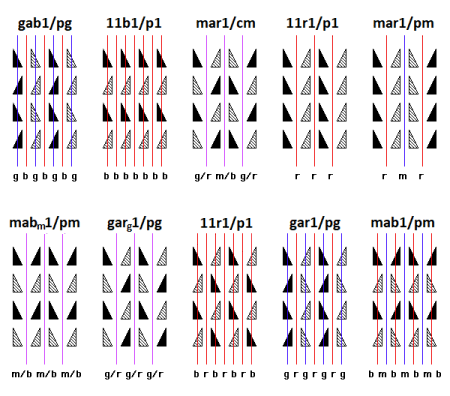
ten-types2

[The existence of only $13$ possible types for rotationless pie patterns — the $10$ ‘two-colored’ types shown above (g-b, b-b, m/b-g/r, r-r, m-r, m/b-m/b, g/r-g/r, r-b, g-r, m-b) together with the $3$ ‘one-colored’ types (m-m, g-g, m-g) — is not that hard to establish, and it should be a first step for a new geometrical classification of pie patterns. (Further, the only way to set the two $11r1/p1$ pie patterns above apart from each other is to observe that one is of r-r type and the other is of r-b type!) Indeed this post’s approach relies heavily on the geometrical classification of the $46$ two-colored wallpaper patterns, as well as on the geometrical classification of the $17$ one-colored wallpaper patterns, presented in Chapters 6 and 8 of ISOMETRICA; my future goal is a ‘combined’ approach that would depart from the $13$ rotationless pie patterns and move on to richer types, examining which ‘roads’ of mutually parallel vertical (glide) reflections and horizontal twofold (glide) rotations could pass through ‘forrests’ of vertical rotations and rotoreflections — much in the spirit of Chapter 8 of ISOMETRICA, where I examine how (glide) reflection axes of the three rotationless wallpaper patterns ( $pm$ , $pg$ , $cm$ ) could pass through lattices of rotation centers, giving rise to richer types.]

There exist 63 two-colored wallpaper patterns, 17 of which may be viewed as one-colored … in the sense that, although the two colors are in perfect symmetry — or rather ‘balance’ — with each other, there are no color-reversing isometries: such wallpaper patterns correspond to pie patterns having no level-swapping isometries (roots m11, g11, 111), yielding therefore excellent (‘quasi-symmetric’) examples for the $17$ types of (III). These $17$ pie patterns I list, in direct analogy to (I), right below (with a corresponding example from ISOMETRICA in brackets):

m11 (vertical reflection):

$m111/pm$ [Fig. 6.15]

$m111/cm$ [Fig. 6.25]

$m112/pmm$ [Fig. 6.70]

$m112/cmm$ [Fig. 6.80]

$m112/pmg$ [Fig. 6.61]

$m114/p4g$ [Fig. 6.109]

$m114/p4m$ [Fig. 6.117]

$m113/p31m$ [Fig. 6.122]

$m113/p3m1$ [Fig. 6.125]

$m116/p6m$ [Fig. 6.138]

g11 (vertical glide reflection):

$g111/pg$ [Fig. 6.4]

$g112/pgg$ [Fig. 6.48]

111:

$1111/p1$ [Fig. 6.8]

$1112/p2$ [Fig. 6.5]

$1114/p4$ [Fig. 6.100]

$1113/p3$ [Fig. 6.121]

$1116/p6$ [Fig. 6.129]

Unfortunately the situation is not that simple in (II): not only because several of the ‘plausible’ $68$ types may not be possible (as already hinted on), but also because of situations like the one described below (where the same 4-root (mar2) and the same cross pattern ( $pmg$ ) may generate distinct pie patterns):

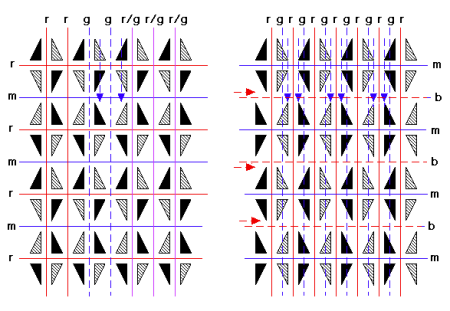
pb'gm-pc'mg

[The pattern on the left, to be named $mar_g2/pmg$ right below, has vertical reflection (m) in one (‘horizontal’) direction and horizontal twofold rotation (r) in two directions; there also exists vertical glide reflection (g) along both kinds of ‘vertical’ horizontal twofold rotations (r), indicated by g/r. The pattern on the right, to be named $mar2/pmg$ right below, has vertical reflection (m) with ‘in-between’ horizontal twofold glide rotation (b) in one (‘horizontal’) direction, and horizontal twofold rotation (r) with ‘in-between’ vertical glide reflection (g) in the other (‘vertical’) direction. (Global isometries are shown in blue lines (solid for vertical reflection (m), dotted for vertical glide reflection (g)), level-swapping isometries are shown in red lines (solid for horizontal twofold rotation (r), dotted for horizontal twofold glide rotation (b)), and the ‘mixed’ case g/r is shown in solid purple lines. Both patterns share vertical twofold rotation and vertical twofold rotoreflection, not shown above; their axes pass through color-preserving centers and color-reversing centers, respectively, found at the intersections of perpendicular lines.)]

It is therefore prudent at this point to save the $17$ roots mainly for notational purposes, and simply follow the route opened by the one-to-one correspondence between pie patterns and two-colored wallpaper patterns. Below I provide a list of the $46$ type II pie patterns by root & cross pattern and under both the ‘root name’ and the corresponding two-colored wallpaper pattern type — as recorded in both SYMMETRIES OF CULTURE and ISOMETRICA — with the ‘broader’ (one-colored) wallpaper type in brackets:

mar (vertical reflection, horizontal glide reflection, horizontal twofold rotation):

$mar1/cm$ = $c'm$ [ $pm$ ]

$mar1/pm$ = $p_b'1m$ [ $pm$ ]

$mar2/pmm$ = $p_b'mm$ [ $pmm$ ]

$mar2/cmm$ = $c'mm$ [ $pmm$ ]

$mar2/pmg$ = $p_c'mg$ [ $cmm$ ]

$mar_g2/pmg$ = $p_b'gm$ [ $pmm$ ]

$mar4/p4g$ = $p_c'4gm$ [ $p4m$ ]

$mar4/p4m$ = $p_c'4mm$ [ $p4m$ ]

mab (vertical reflection, horizontal glide reflection, horizontal twofold glide rotation):

$mab1/pm$ = $p_c'm$ [ $cm$ ]

$mab_m1/pm$ = $p_b'm$ [ $pm$ ]

$mab2/pmm$ = $p_c'mm$ [ $cmm$ ]

$mab2/pmg$ = $p_b'mg$ [ $pmg$ ]

gar (vertical glide reflection, horizontal glide reflection, horizontal twofold rotation):

$gar1/pg$ = $p_c'g$ [ $cm$ ]

$gar_g1/pg$ = $p_b'g$ [ $pm$ ]

$gar2/pgg$ = $p_c'gg$ [ $cmm$ ]

$gar_g2/pgg$ = $p_b'gg$ [ $pmg$ ]

gab (vertical glide reflection, horizontal glide reflection, horizontal twofold glide rotation):

$gab1/pg$ = $p_b'1g$ [ $pg$ ]

m1r (vertical reflection, horizontal twofold rotation):

$m1r\bar{2}/pm$ = $pmm'$ [ $pmm$ ]

$m1r\bar{2}/cm$ = $cmm'$ [ $cmm$ ]

$m1r\bar{4}/pmm$ = $p4'mm'$ [ $p4m$ ]

$m1r\bar{4}/cmm$ = $p4'm'm$ [ $p4m$ ]

$m1r\bar{6}/p31m$ = $p6'm'm$ [ $p6m$ ]

$m1r\bar{6}/p3m1$ = $p6'mm'$ [ $p6m$ ]

m1b (vertical reflection, horizontal twofold glide rotation):

$m1b\bar{2}/pm$ = $pmg'$ [ $pmg$ ]

$m1b\bar{4}/cmm$ = $p4'g'm$ [ $p4g$ ]

g1r (vertical glide reflection, horizontal twofold rotation):

$g1r\bar{2}/pg$ = $pm'g$ [ $pmg$ ]

$g1r\bar{4}/pgg$ = $p4'gm'$ [ $p4g$ ]

g1b (vertical glide reflection, horizontal twofold glide rotation):

$g1b\bar{2}/pg$ = $pgg'$ [ $pgg$ ]

1a1 (horizontal glide reflection):

$1a11/p1$ = $p_b'1$ [ $p1$ ]

$1a12/p2$ = $p_b'2$ [ $p2$ ]

$1a14/p4$ = $p_c'4$ [ $p4$ ]

11r (horizontal twofold rotation):

$11r1/p1$ [r-r]= $pm'$ [ $pm$ ]

$11r1/p1$ [r-b]= $cm'$ [ $cm$ ]

$11r2_b/p2$ = $pm'g'$ [ $pmg$ ]

$11r2_r/p2$ = $pm'm'$ [ $pmm$ ]

$11r2_{rb}/p2$ = $cm'm'$ [ $cmm$ ]

$11r4/p4$ = $p4g'm'$ [ $p4g$ ]

$11r4_r/p4$ = $p4m'm'$ [ $p4m$ ]

$11r3/p3$ = $p31m'$ [ $p31m$ ]

$11r3_r/p3$ = $p3m'$ [ $p3m1$ ]

$11r6/p6$ = $p6m'm'$ [ $p6m$ ]

11b (horizontal twofold glide rotation):

$11b1/p1$ = $pg'$ [ $pg$ ]

$11b2/p2$ = $pg'g'$ [ $pgg$ ]

111:

$111\bar{2}/p1$ = $p2'$ [ $p2$ ]

$111\bar{4}/p2$ = $p4'$ [ $p4$ ]

$111\bar{6}/p3$ = $p6'$ [ $p6$ ]

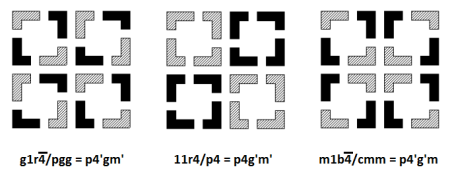
The subscripts in our list indicate the isometry on which the subscripted isometry lies (or passes through); such ‘subscript’ information is provided only for disambiguation purposes, specifically to distinguish $p_b'gm$ from $p_c'mg$ , $p_b'm$ from $p_c'm$ , $p_b'g$ from $p_c'g$ , $p_b'gg$ from $p_c'gg$ , $p4m'm'$ from $p4g'm'$ , $p3m'$ from $p31m'$ , and, last but not least, $pm'g'$ AND $pm'm'$ from $cm'm'$ : the last three types share $p2$ as their cross pattern, so a double subscript for $cm'm'$ becomes necessary exactly as the diagram below indicates.

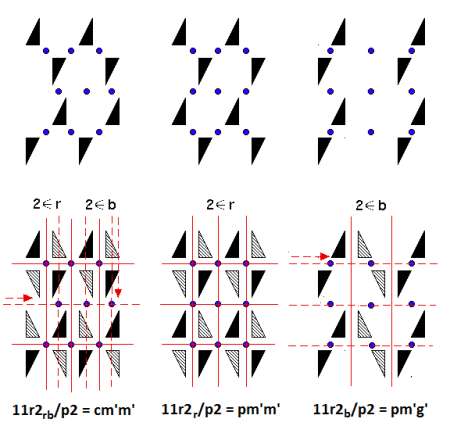
p2111
Although there is no need for disambiguation in this case, the ‘double’ (two-level) diagrams below show the three types sharing $p3$ as their cross pattern:

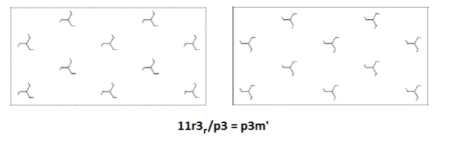p3m11 Three kinds of vertical threefold rotation axes, all of them intersecting horizontal twofold rotation axes, one of them passing through centers of ‘tripods’.

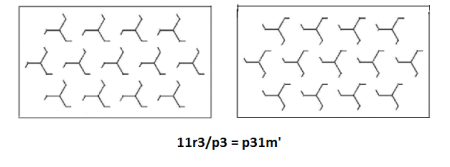p31m Two kinds of vertical threefold rotation axes, one of them intersecting horizontal twofold rotation axes and passing through centers of ‘tripods’.

p6'

Vertical sixfold rotoreflection axes passing through the centers of ‘tripods’, ‘free’ vertical threefold rotation axes.

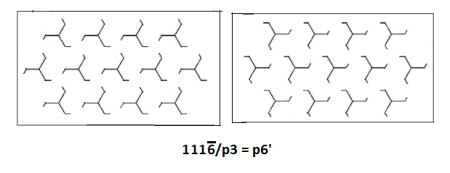
Next come the three types that, although of distinct cross patterns, belong to the $p4g$ family (when viewed as two-colored wallpaper patterns, that is):

p4g3

$g1r\bar{4}/pgg$ = $p4'gm'$ : vertical glide reflection in two (‘diagonal’) directions, horizontal twofold rotation and horizontal twofold glide rotation in the other two directions, vertical fourfold rotoreflection, ‘free’ vertical twofold rotation.

$11r4/p4$ = $p4g'm'$ : horizontal twofold rotation and horizontal twofold glide rotation in two directions, horizontal twofold glide rotation in the other two (‘diagonal’) directions, vertical fourfold rotation, ‘free’ vertical twofold rotation.

$m1b\bar{4}/cmm$ = $p4'g'm$ : vertical reflection and vertical glide reflection in two directions, horizontal twofold glide rotation in the other two (‘diagonal’) directions, vertical fourfold rotoreflection, ‘free’ vertical twofold rotation.

We conclude with the two type II pie patterns that have $p4g$ and $p4m$ as their cross pattern, shown in both ‘double’ and ‘unified’ form:

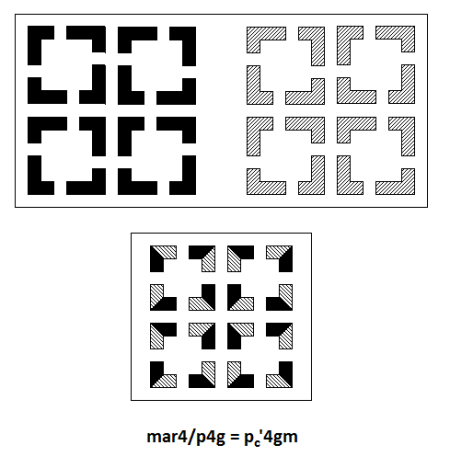pc4gm-gammas Vertical reflection with horizontal twofold glide rotation along ( $b\in m$ ) and in-between horizontal twofold rotation in two (‘vertical’ – ‘horizontal’) directions; horizontal twofold rotation and in-between vertical glide reflection in the other two (‘diagonal’) directions; vertical fourfold rotation, vertical fourfold rotoreflection, vertical twofold rotoreflection.

mar4

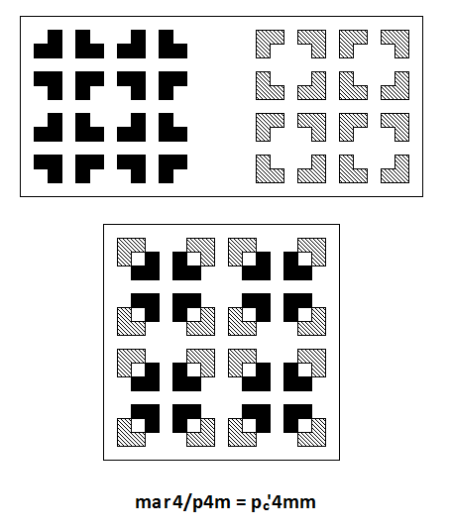
Vertical reflection with horizontal twofold glide rotation along ( $b\in m$ ) in two (‘diagonal’) directions; in-between vertical glide reflection with horizontal twofold rotation along ( $r\in g$ ) in the same two (‘diagonal’) directions; vertical reflection with in-between horizontal twofold glide rotation in the other two (‘vertical’-‘horizontal’) directions; vertical fourfold rotation, vertical fourfold rotoreflection, vertical twofold rotoreflection.

[A pie pattern of same type appears early in this post, but what is ‘diagonal’ here (m/b–g/r) is ‘vertical’-‘horizontal’ there, and what is ‘diagonal’ there (m–b) is ‘vertical’-‘horizontal’ here.]

The reader may find many additional examples of type II patterns, in the form of two-colored wallpaper patterns, in both Chapter 5 of SYMMETRIES OF CULTURE (patterns classified by way of flow charts) and Chapter 6 of ISOMETRICA (patterns clasified by way of symmetry plans). (Please note that in my book I mistakenly use $p'm$ instead of $p_b'm$ (as I discovered only on 9/17/17) 🙂 )

[A good project left to the reader is to verify, following our approach, that there exist precisely $7+17+7=31$ “stick patterns” (three-dimensional analogues of border patterns with border patterns as their cross sections, also known since the late 1920’s); the needed material on two-colored border patterns may be found in both Chapter 4 of SYMMETRIES OF CULTURE and Chapter 5 of ISOMETRICA.]

I would like to dedicate this post to Dorothy Washburn and Donald Crowe: their SYMMETRIES OF CULTURE inspired me to introduce two-colored wallpaper patterns to SUNY Oswego’s MAT 103 (from the very first time I taught it in Fall 1995) and to write Chapter 6 of ISOMETRICA (during three unforgettable weeks in January 2000).

ADDENDUM (8/25/2018): the following clarification concerns the writing in red above!

Sadly, and noticed only after posting this article, two pie patterns ended up having the same name, $11r1/p1$ ! I have already commented on this accident (in red), but would like to further elaborate below.

The cross patterns of the two pie patterns, $11r1/p1$ [r-r] = $pm'$ (horizontal twofold rotation) and $11r1/p1$ [r-b] = $cm'$ (horizontal twofold rotation and horizontal twofold glide rotation), are of $p1$ type. But these are not ‘arbitrary’ $p1$ patterns: they both have translation in two perpendicular directions (something not always true in a $p1$ ). Further, in the $p1$ cross pattern of the r-b pie pattern there is a ‘diagonal’ translation that is not composition of two valid translations in the said two perpendicular directions, whereas this is not the case for the $p1$ cross pattern of the r-r pie pattern! One way to remove the said ambiguity is to set $11r1/p1$ [r-b] = $11r1/p1$ * and $11r1/p1$ [r-r] = $11r1/p1$ ** … recognizing thus two special subcategories of $p1$ , that is $p1$ * (perpendicular translations not generating all translations) and $p1$ ** (perpendicular translations generating all translations).

[Although we do not need this for disambiguation purposes, let us mention here that we could in the same way consider/define a subcategory of $p2$ , denoted by $p2$ ** and referring to those $p2$ wallpaper patterns where the half turn centers form rectangles rather than merely parallelograms. This ‘ruling’ of half turn centers may certainly happen even in the absence of glide reflection, see for example 8.2.1 and 8.2.2 in ISOMETRICA. As for the ‘ruling’ of ‘units’ in $11r1/p1$ * and $11r1/p1$ **, and the said existence of perpendicular translations in their cross pattern, that is a result of the existence of horizontal twofold rotation in them … in about the same way that reflection in a $pm$ yields translation not only perpendicular to it (by mere composition), but also — see for example 6.3.4 in ISOMETRICA — parallel to it! And the more subtle difference between $p1$ * and $p1$ ** could be explained in a manner entirely analogous to the difference between $cm$ and $pm$ , having to do with the analysis or not of ‘diagonal’ translations into valid ‘vertical’ and ‘horizontal’ translations — see 8.1.9 in ISOMETRICA. (We note here — and in relation to ISOMETRICA 8.1.9 again (and stressing the ‘affinity’ between $pm$ and $pg$ ) — that the cross pattern of $11b1/p1$ = $pg'$ is always a $p1$ **, whereas the cross pattern of $1a11/p1$ = $p_b'1$ or $111\bar{2}/p1$ = $p2'$ may well be an ‘arbitrary’ $p1$ … in about the same way the cross pattern of $1a12/p2$ = $p_b'2$ may well be an ‘arbitrary’ $p2$ .)]

This entry was posted on September 30, 2017 at 10:29 am and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

crystallomath

80 pie patterns

Leave a comment Cancel reply

crystallomath

80 pie patterns

Share this:

Related

Leave a comment Cancel reply